计算机掷骰子吗？关于随机数的一些细节

原理研究
,

在计算机领域，随机数是一个十分重要的机制，除了模拟客观世界的随机现象，有一些场景本身就需要随机数，比如 AES 对称机密算法中需要一个随机数作为密钥，以及 TCP 连接”三次握手“时 TCP 头的 seq 字段应该初始化为随机值。对于人类来说，人脑无法凭空创造出随机数，至少无法证明构思的数字是一个随机数，人类只能借助硬币和骰子等工具来得到一个随机的数字。作为在计算方面比人脑更强大的计算机，能否创造出随机数呢，还是计算机也需要“骰子”呢？

Random 与真伪随机

在需要随机数时，熟悉 Java 的开发者很容易基于 java.util.Random 写出如下代码：

1
2
Random random = new Random();
int ri = random.nextInt();

此外，也可以指定其它随机数字类型。

1
2
3
4
5
6
boolean rb = random.nextBoolean();
long rl = random.nextLong();
float rf = random.nextFloat();
double rd = random.nextDouble();
byte[] rndBytes = new byte[16];
random.nextBytes(rndBytes);

阅读 Random 类的源代码，我们会发现这些 nextXXX 方法获取随机值时都会调用该类的另一个 next 方法。

1
2
3
4
5
6
7
8
9
10
// jdk 1.8 java.util.Random
protected int next(int bits) {
    long oldseed, nextseed;
    AtomicLong seed = this.seed;
    do {
        oldseed = seed.get();
        nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.compareAndSet(oldseed, nextseed));
    return (int)(nextseed >>> (48 - bits));
}

next 方法包含了 Random 类生成随机数的核心逻辑。不过，在解释这段代码之前，我们先了解一个前置知识——LCG 算法。

LCG 算法

LCG（Linear congruential generator，线性同余生成器）算法是一种利用数学公式来计算随机数的算法，原理可以概括为一个简单的公式。

$$
X_{n+1} = (aX_{n} + c)\ mod\ m
$$

  • $X$ 代表一个整数序列，是一系列随机数，满足 $0 \leq X_{n} < m$。
  • $m$ 是模数，满足 $0 < m$。
  • $a$ 是乘数，满足 $0 < a < m$。
  • $c$ 是增量，$0 \leq c < m$。
  • $X_{0}$ 是序列起始值，又称种子数，满足 $0 \leq X_{0} < m$。

线性同余公式相当于将线性函数 $f(x)=ax+c$ 的值对 $m$ 取模，然后将结果的余数作为新的输入来计算下一个余数，如此反复，得到的结果集构成了一个序列，这个序列的值分布相当分散，符合了随机数分布均匀的特点，因此可以用来生成随机数。LCG 算法正是基于这个序列实现了生成随机数的功能，但并非直接可用，还需要解决两个额外的问题。

首先，线性同余公式本身具备幂等性，在 $m$、$a$、$c$ 不变的情况下，对于相同的 $X_{n}$，总能得到相同的 $X_{n+1}$。一旦 $X_{n}$ 中出现重复值，序列中也会出现重复段，这将导致 $X$ 呈现周期性的特点，而随机序列不应该有周期。为了解决这个问题，LGC 算法必须消除周期的影响。

参数 起始值 序列
m = 9, a = 2, c = 0 1 1,2,4,8,7,5,1,…
m = 9, a = 2, c = 0 3 3,6,3,…
m = 9, a = 2, c = 0 5 5,1,2,4,8,7,5,…
m = 9, a = 4, c = 1 0 0,1,5,3,4,8,6,7,2,0,…

不言自明，序列的周期由 $m$、$a$、$c$ 的值控制，$m$ 是序列中元素取值的上限，也就是周期范围的上限。调整这三个常数，设置一个很大的周期，比如 $2^{31}$，只在这个范围内取值，可以保证得到的数是随机数，而且这个范围也不算小，足以使用很长一段时间。

其次，线性同余的结果容易被逆向推算出来。两个连续的值可以推断出 $a$ 和 $c$，多个连续的值可以猜测出 $m$。一旦知道 $m$、$a$、$c$ ，就可以根据当前值计算出下一个值，这将导致严重的后果：下一个随机数可以被预测！解决起来也简单，只对外暴露 $X_{n+1}$ 的部分数位，完整值仅在内部使用。一般会暴露高位，因为高位随机特点更鲜明。

解决了以上两个问题，就可以基于 LCG 算法实现一个随机数生成器，不考虑并发问题，代码比较简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private static final long multiplier = 0x5DEECE66DL;
private static final long modulus = 1L << 48;
private static final long addend = 0xBL;

private long seed;

public int nextRandom() {
    // 每次计算后更新 seed
    this.seed = lcg(modulus, multiplier, addend, this.seed);
    // seed 的有效位为 0 到 47，高 16 位为 0，右移 16 位代表仅返回 seed 的 16 到 47 位
    return (int) (seed >>> 16);
}

protected long lcg(long m, long a, long c, long seed) {
    return (seed * a + c) % m;
}

LCG 算法是最古老最常见的伪随机数生成算法之一，因为其简便易行的特点，积极活跃于计算机世界之中，大部分编程语言都提供了 LCG 算法实现的随机数 API。

编程语言 $m$ $a$ $c$ 对外范围
glibc（GCC） 2^31 1103515245 12345 位 30..0
java.util.Random 2^48 25214903917 (5DEECE66D 16 ) 11 位 47..16
Virtual Pascal 2^32 134775813 1 位 63..32

java.util.Random

现在再来看 Random 类的 next 方法，大致与上面的 LCG 算法相同，细微之处有两点差异。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// jdk 1.8 java.util.Random
private final AtomicLong seed;

private static final long multiplier = 0x5DEECE66DL;
private static final long addend = 0xBL;
private static final long mask = (1L << 48) - 1;

protected int next(int bits) {
    long oldseed, nextseed;
    // 原子类循环 CAS，从而实现并发安全更新 seed 的值
    AtomicLong seed = this.seed;
    do {
        oldseed = seed.get();
        // 相当于 nextseed = (oldseed * multiplier + addend) % (1L << 48)
        nextseed = (oldseed * multiplier + addend) & mask;
    } while (!seed.compareAndSet(oldseed, nextseed));
    // nextInt() 方法传入的 bits 参数为 32
    return (int)(nextseed >>> (48 - bits));
}

首先，Random 类为了支持并发，使用原子类型 AtomicLong 保存 seed 的值，辅以循环 CAS 的方式保证了并发环境下每个线程更新 seed 的操作都是原子性操作，不会存在多线程互相覆盖的情况。循环 CAS 是一种常见的并发技巧，seed.compareAndSet(oldseed, nextseed) 更新时如果 seed 中的值不等于 oldseed，就会放弃更新并返回 false，于是重新进入 do-while 循环体，获取最新的 seed 再次计算。循环 CAS 确保了线程的操作一定基于共享变量的最新状态进行，并保证线程对共享变量的更新一定有效。

其次，Random 采取了 power of two 的技巧来优化模运算。当模数为 2 的 n 次方时，可以用位与运算来替代模运算，基本公式为 $i\ mod\ 2^{n} = i\ &\ (2^{n} - 1)$，比如 i % 8 == i & 7、i % 16 == i & 15、i % (1 << 16) == i & ((1 << 16) - 1)。因为 2 的 n 次方减 1 的二进制表示是连续 n-1 个 1，相当于一个掩码，一个数与掩码位与的结果就是这个数在掩码所有为 1 的数位上的值，所以右边的位与计算可以求出 $i$ 在 $2^{n} - 1$ 这个范围内的值。对于左边的模运算，$i$ 大于等于 $2^{n}$ 的部分都会被除去，结果也是 $i$ 在 $2^{n} - 1$ 这个范围内的值。两种计算方式等价，但 CPU 执行位与指令时比执行模运算相关指令更快，可以提高计算效率。这个优化技巧的应用很广，比如 HashMap 也有用到。HashMap 内部数组初始化时长度固定为 2 的整数幂，扩容时也是成倍扩容，正是为了保证数组长度一定是 2 的 n 次方，从而在计算 key 的数组下标时可以将模运算替换为位与操作。

种子

LGC 算法中，在常量 $m$、$a$、$c$ 确定的情况下，输入相同的起始值 $X_{0}$ 就能得到相同的序列，这样随机数生成器就有了“回放”的功能。Random 类也支持“回放”功能，可以在构造函数传入一个 long 类型的“种子”。两个不同 Random 对象，种子相同，生成的随机数序列也相同。同一个种子，同一个序列。

1
2
3
4
5
6
7
8
long seed = -229985452L;
Random rnd1 = new Random(seed);
Random rnd2 = new Random(seed);
assertThat(rnd1.nextInt()).isEqualTo(rnd2.nextInt());
assertThat(rnd1.nextBoolean()).isEqualTo(rnd2.nextBoolean());
assertThat(rnd1.nextLong()).isEqualTo(rnd2.nextLong());
assertThat(rnd1.nextFloat()).isEqualTo(rnd2.nextFloat());
assertThat(rnd1.nextDouble()).isEqualTo(rnd2.nextDouble());

基于“回放”的特点，可以实现一些比较奇怪的代码，比如“生成的随机字符串竟是一个有意义的单词”。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
@Test
void random_string_equals_hello() {
    long seed = -229985452L;
    assertThat(randomString(seed)).isEqualTo("hello");
}

String randomString(long seed) {
    Random rnd = new Random(seed);
    StringBuilder sb = new StringBuilder();
    while (true) {
        int i = rnd.nextInt(27);
        if (i == 0) {
            break;
        }
        // '`' 符号是 ascii 表里小写字母 'a' 的前一位
        sb.append((char) ('`' + i));
    }

    return sb.toString();
}

随机生成了 hello 字符串！看起来十分新奇，实际上这代码中的随机数种子 -229985452L 是提前计算好的，换个值就不成立了。这种“新奇”只是随机数种子的应用。

源码上，如果 Random 类的构造函数传入了参数 seed，还会先进行一次混淆处理，这样保证了随机性，同时也保证种子数不会超过模数 $2^{48}$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// jdk 1.8 java.util.Random
public Random(long seed) {
    if (getClass() == Random.class)
        this.seed = new AtomicLong(initialScramble(seed));
    else {
        // subclass might have overriden setSeed
        this.seed = new AtomicLong();
        setSeed(seed);
    }
}

private static long initialScramble(long seed) {
    return (seed ^ multiplier) & mask;
}

如果没有指定种子，Random 类的策略是随机生成一个新种子。生成新种子时考虑了系统时间，这是一个随机量，同时还有一个原子类型 seedUniquifier 用于记录上一次生成的种子，新的种子由这两个因素决定。原子变量 seedUniquifier 采用了循环 CAS 的方式保证并发安全更新，其初始值为一个魔法值，计算新种子时的乘数 181783497276652981L 也是一个魔法值，这两个魔法值来自注释上的那篇论文 L’Ecuyer, “Tables of Linear Congruential Generators of Different Sizes and Good Lattice Structure”, 1999。Random 的种子生成算法参考了这篇论文，保证了并发调用时生成的随机数种子也具备很好的随机性。（实际上根据这篇论文，乘数的值应该为 1181783497276652981L，这里少了最高位的 1，可能是复制时漏掉了。这个 bug 在 JDK 11 中已经修复。）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// JDK 1.8
public Random() {
    this(seedUniquifier() ^ System.nanoTime());
}

private static final AtomicLong seedUniquifier
        = new AtomicLong(8682522807148012L);
private static long seedUniquifier() {
    // L'Ecuyer, "Tables of Linear Congruential Generators of
    // Different Sizes and Good Lattice Structure", 1999
    for (;;) {
        long current = seedUniquifier.get();
        long next = current * 181783497276652981L;
        if (seedUniquifier.compareAndSet(current, next))
            return next;
    }
}

具备“回放”功能的随机数生成器用途也非常广泛。许多随机地图的游戏，比如文明、Minecraft、饥荒，玩家之间会共享一些趣味性很高的地图，而共享的途径就是一个称为地图种子的数字。不难推测，这些游戏都是用了随机数生成器生成的随机序列作为游戏地图的初始化参数，利用随机数来构建各个元素，从而创造出一个随机的世界。如果载入游戏时指定了地图种子，能可以生成一个既定的参数列表，呈现出一个已知的地图；如果没有指定，系统会随机生成一个地图种子，创造出一个随机地图。某种意义上，随机数种子就像游戏世界创世之初的奇点，计算机从这个奇点中孕育出了一个全新的世界。

真伪随机

除了 LGC 算法，常用的随机数生成算法还有平方取中法、梅森旋转算法等，都是利用数学生成周期性序列的方法，我们称之为伪随机数。因为这些随机序列看起来随机，实际上并不随机，受限于有限的状态，具备周期性这个显著的缺点。

冯·诺依曼曾经断言：任何用数学方法生成随机数的尝试都不合理。

与数学上的伪随机数相对，现实世界在自然随机性中产生的随机数，称为真随机数。真随机不仅看起来随机，实际上也随机。真随机序列分布均匀，不可预测，还没有周期，是真正符合传统认知的随机数。产生真随机数的机制没有幂等性，所有条件相同的情况下，输出也可能不相等。这就是真随机的魅力。无论两次投掷的角度和力道如何相同，物理学灵巧的手指也可能把骰子拨到一个截然不同的点数。在安全领域，幂等性是所有伪随机数生成算法无法掩盖的阿喀琉斯之踵。因为图灵机本身就是充满确定性的工具，只要计算机还在采用图灵机作为计算模型，就无法凭空创造出不确定性的真随机。

既然如此，计算机就无法生成真随机数了吗？

计算机系统的设计者们采取了一个十分巧妙的方式，既然无法凭空创造出真随机，那就直接使用现实世界的随机源。计算机可以直接使用的真随机源其实并不多：

  • 时钟，每一个操作发生时的纳秒时间戳具备很强的随机性。前面 Random 类生成随机种子时就是利用了时钟的随机性。

  • 硬件，计算机与外界交互都是依托于硬件，鼠标的移动距离和间隔、键盘的敲击间隔、网卡等待时长、磁盘调度间隔，都是非常随机的数据。这里列出一些可以作为计算机真随机的来源：

    • 键盘
    • 鼠标
    • 中断请求
    • 机械硬盘寻道时长
    • 网络活动
    • 麦克风
    • 网络摄像头
    • 触摸屏
    • WIFI
    • 以及一些特殊硬件

    计算机借助这些硬件，从现实世界汲取随机性，生成真随机数。这些硬件便是计算机的“骰子”。

/dev/random

Unix 系的系统有一个 /dev/random 文件，读取到的内容是一些随机字节，这些随机字节都来自系统的熵池。所谓熵池，通俗讲就是一个随机字节的资源池。这个池子里存放着系统从硬件采集来的真随机信息，当程序需要真随机数时可以直接从池子取数。/dev/random 是系统提供的熵池入口，还有另一个入口 /dev/urandom，也起着同样的作用。

既然是资源，自然可能耗尽，这两个熵池入口的主要区别，就在于资源耗尽时的处理机制。

  • /dev/random 在资源耗尽时会阻塞，直到系统重新采集到足够的随机字节，阻塞间隔可能长达几分钟。记住，/dev/random 存在线程阻塞风险，后面会介绍这个问题。
  • /dev/urandom 在资源耗尽时不会阻塞，而是退化为伪随机数生成器。

在一些编程习惯里，/dev/random 用于获取随机种子，也可用于生成高随机性的公钥或一次性密码本，而 /dev/urandom 则用于获取随机数。Linux 系统的程序在需要真随机数时，如果没有其它获取方式，基本上都会考虑从熵池中获取。

在容器化的浪潮中，熵池又面临着新的问题。熵池的数据来自硬件，容器启动时熵池是空的，需要一点时间来积累。如果启动时就需要读取熵池，会导致阻塞或启动失败，比如 Docker 日志 crypto/rand: blocked for 60 seconds waiting to read random data from the kernel，就是因为容器刚启动熵池资源不够，Docker 只能暂停一分钟给容器以搜集时间。此时可以考虑主动进行熵注入，一般有两个方向：

  • 在容器外用专门的熵服务器进行“授粉”；
  • 在容器内利用 haveged 进程为熵池提供数据。

SecureRandom 与密码学安全的伪随机序列

密码学领域，对随机数除了随机性要求，还必须保证不可预测。大多数伪随机数生成算法都不符合要求。如 LCG 算法，知道了初始种子，就等于知道了确切的随机序列，攻击者就可以根据当前随机值预测出下一个随机数。LCG 算法实现都不得不将种子作为程序的内部状态保存起来，如 Random 类的 seed 实例属性，就保存着当前的随机数种子。这些内部状态存在着被泄露的可能，攻击者可以通过反射、Unsafe 等方式获取到种子数。密码学需要更不确定的随机数。

对此，JDK 提供了 java.security.SecureRandom 作为更安全的随机数生成器。

SecureRandom 的使用

使用方面，SecureRandom 继承自 java.util.Random，提供的 API 与 Random 大致相同，但有一个功能与 Random 截然相反。SecureRandom 类虽然支持指定种子，但种子只是对现有种子的补充，而非完全替代，因此不具备 Random 的“回放”功能。

1
2
3
4
5
6
7
byte[] rndBytes = new byte[]{7, 11, 13, 17, 19, 23, 29};
SecureRandom sr1 = new SecureRandom(rndBytes);
SecureRandom sr2 = new SecureRandom(rndBytes);
assertThat(sr1.nextInt()).isNotEqualTo(sr2.nextInt());
assertThat(sr1.nextLong()).isNotEqualTo(sr2.nextLong());
assertThat(sr1.nextFloat()).isNotEqualTo(sr2.nextFloat());
assertThat(sr1.nextDouble()).isNotEqualTo(sr2.nextDouble());

SecureRandom 的实现

实现适合密码安全领域的随机数生成器，通常有两个方向：

  • 直接使用真随机数生成器生成的随机数，比如前面提到的系统熵池；

  • 采取满足密码学需求的伪随机数算法，并使用真随机数做种子。

SecureRandom 类在实现上兼顾了上述两种思路，既读取系统熵池，也内置了一个伪随机数算法，最终提供的随机数是两种生成方式结果的混合。

SecureRandom 类的大致结构图如下：

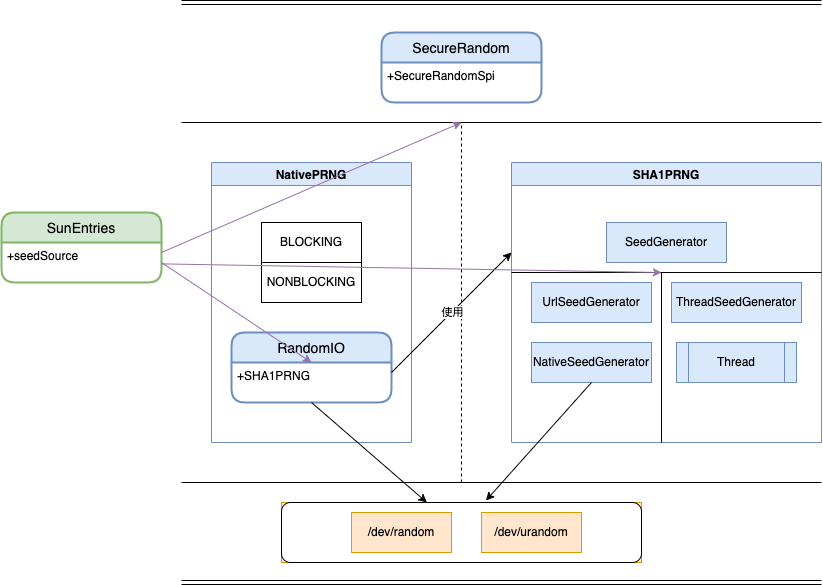
SecureRandom 结构

以下分别介绍这些组成部份。

首先，SecureRandom 在设计上就支持多种随机数生成算法，利用 SPI 机制将算法变为可配置式。SecureRandom 重写了 next 方法，仅仅负责将 nextBytes() 方法提供的随机字节转换为 int 整数，将生存随机数据的职责交给了 nextBytes()，而 nextBytes() 则调用 SPI 实现类 SecureRandomSpi 来获取随机字节。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class SecureRandom extends java.util.Random {

    private SecureRandomSpi secureRandomSpi = null;

    @Override
    final protected int next(int numBits) {
        // 职责转移之后 next 方法只是一个根据字节数组
        // 生成对应 int 类型整数的算法

        int numBytes = (numBits+7)/8;
        byte b[] = new byte[numBytes];
        int next = 0;

        nextBytes(b);
        for (int i = 0; i < numBytes; i++) {
            next = (next << 8) + (b[i] & 0xFF);
        }

        return next >>> (numBytes*8 - numBits);
    }

    @Override
    public void nextBytes(byte[] bytes) {
        // 由 SPI 实现类负责提供随机字节
        secureRandomSpi.engineNextBytes(bytes);
    }
}

所以，要了解 SecureRandom 的原理，需要深入了解 SecureRandomSpi 的实现类。JDK 为 SecureRandomSpi 提供了四种实现。

  • SHA1PRNG，内置的伪随机数生成算法，基于 SHA1 哈希算法生成随机数，对应实现类为 sun.security.provider.SecureRandom。SHA1PRNG 算法是 Sun 公司的专利算法，以 OracleJDK 为准，其它 JDK 平台的实现不一致。

  • NativePRNG，使用系统熵池，对应实现类为 sun.security.provider.NativePRNG。Unix-Like 系统和 Windows 的实现不一致，Unix 系列的系统使用 /dev/random 作为种子来源，/dev/urandom 作为真随机数来源，Windows 平台的 NativePRNG 类则不具备实际意义，只是一个不提供任何功能的 dummy 实现，Windows 的 SecureRandom 类会优先使用 SHA1PRNG 算法，只在获取种子时通过 NativeSeedGenerator 类中调用系统 API CryptoAPI 来获取种子。

  • NativePRNGBlocking，NativePRNG 的特殊版本，对应实现类 sun.security.provider.NativePRNG$Blocking，指定 /dev/random 同时作为种子来源和真随机数来源。

  • NativePRNGNonBlocking，NativePRNG 的特殊版本，对应实现类 sun.security.provider.NativePRNG$NonBlocking，指定 /dev/urandom 同时作为种子来源和真随机数来源。

SecureRandom 在构造函数初始化 SecureRandomSpi 属性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class SecureRandom extends java.util.Random {
    private SecureRandomSpi secureRandomSpi = null;

    public SecureRandom() {
        super(0);
        getDefaultPRNG(false, null);
    }

    public SecureRandom(byte seed[]) {
        super(0);
        getDefaultPRNG(true, seed);
    }

    /** 初始化 secureRandomSpi */
    private void getDefaultPRNG(boolean setSeed, byte[] seed) {
        // 利用 SPI 机制获取实现类
        String prng = getPrngAlgorithm();
        if (prng == null) {
            // 如果没有配置，使用 SHA1PRNG 实现
            // bummer, get the SUN implementation
            prng = "SHA1PRNG";
            this.secureRandomSpi = new sun.security.provider.SecureRandom();
        } else {
            try {
                // 如果有配置，则根据配置选择具体的 NativePRNG 实现
                SecureRandom random = SecureRandom.getInstance(prng);
                this.secureRandomSpi = random.getSecureRandomSpi();
            } catch (NoSuchAlgorithmException nsae) {
                // never happens, because we made sure the algorithm exists
                throw new RuntimeException(nsae);
            }
        }
    }
}

最重要的一步在 getDefaultPRNG() 方法中，String prng = getPrngAlgorithm() 从 JDK 已注册的 Provider 列表中查找第一个类型为 SecureRandom 的 Provider，获取其名称，然后根据该名称去实例化 secureRandomSpi。

负责注册 Provier 的类为 sun.security.provider.SunEntries，在其 putputEntries() 方法中会根据系统配置和系统类型注册不同的 Provider。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
final class SunEntries {
    // seedSource 来源于系统配置
    private static final String seedSource;
    static void putEntries(Map<Object, Object> map) {
        // Windows 平台 JDK 此处返回 false
        boolean nativeAvailable = NativePRNG.isAvailable();
        boolean useNativePRNG = seedSource.equals("file:/dev/urandom") ||
            seedSource.equals("file:/dev/random");

        if (nativeAvailable && useNativePRNG) {
            map.put("SecureRandom.NativePRNG",
                "sun.security.provider.NativePRNG");
        }

        map.put("SecureRandom.SHA1PRNG",
             "sun.security.provider.SecureRandom");
        if (nativeAvailable && !useNativePRNG) {
            map.put("SecureRandom.NativePRNG",
                "sun.security.provider.NativePRNG");
        }

        // Windows 平台 JDK 此处也返回 false
        if (NativePRNG.Blocking.isAvailable()) {
            map.put("SecureRandom.NativePRNGBlocking",
                "sun.security.provider.NativePRNG$Blocking");
        }

        // Windows 平台 JDK 此处也返回 false
        if (NativePRNG.NonBlocking.isAvailable()) {
            map.put("SecureRandom.NativePRNGNonBlocking",
                "sun.security.provider.NativePRNG$NonBlocking");
        }
        // 省略不相关配置
    }
}

seedSource 属性的值来自系统配置，尝试从命令行参数和配置文件中获取熵源偏好。这是个出镜率很高的属性，后面将看到许多类都会参考 seedSource 的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private static final String seedSource;
static {
    seedSource = AccessController.doPrivileged(
        new PrivilegedAction<String>() {

            @Override
            public String run() {
                // Java 启动命令
                String egdSource = System.getProperty("java.security.egd", "");
                if (egdSource.length() != 0) {
                    return egdSource;
                }
                // JDK 配置项
                egdSource = Security.getProperty("securerandom.source");
                if (egdSource == null) {
                    return "";
                }
                return egdSource;
            }
        });
}

综合起来，seedSource 代表系统配置，NativePRNG 类的 isXXXAvailable() 方法代表平台环境，SunEntries 类结合两者进行注册，SecureRandom 则会在初始化时读取对应的注册项，从而实现动态加载 secureRandomSpi。

整个过程中，开发者唯一可控的就是系统配置。如同代码展示的一样，有两个配置项可以决定 SecureRandom 采取的实现：

  • 通过 Java 启动参数 -Djava.security.egd=file:/dev/xxx 指定一个熵池文件，使用 NativePRNG；
  • 通过 JDK 目录下 conf/securety/java.security 文件（或者 JRE 目录 jre/lib/security/java.security）设置配置项 securerandom.source 为 file:/dev/random 或 file:/dev/urandom，使用 NativePRNG，默认配置为 /dev/random。（在 JDK 1.8 之前的版本有个 BUG，使用 urandom 需要设置为 file:/dev/./urandom，JDK 8 已经修复。）

显然，Java 命令行参数的优先级更高。

Windows 平台的 JDK 因为 SunEntries 的 putEntries 方法没有注册对应的 NativePRNG，会直接采取 SHA1PRNG 实现。

NativePRNG 的实现

NativePRNG 有三种实现类，但大同小异，都是依赖于内部单例对象 RandomIO 进行操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public final class NativePRNG extends SecureRandomSpi {
    // RandomIO 的种类
    private enum Variant {
        MIXED, BLOCKING, NONBLOCKING
    }

    // RandomIO 的单例
    private static final RandomIO INSTANCE = initIO(Variant.MIXED);

    // 根据类型创建不同的 RandomIO 对象
    private static RandomIO initIO(final Variant v) {}

    @Override
    protected void engineSetSeed(byte[] seed) {
        INSTANCE.implSetSeed(seed);
    }

    // get pseudo random bytes
    @Override
    protected void engineNextBytes(byte[] bytes) {
        INSTANCE.implNextBytes(bytes);
    }

    // get true random bytes
    @Override
    protected byte[] engineGenerateSeed(int numBytes) {
        return INSTANCE.implGenerateSeed(numBytes);
    }
}

SecureRandomSpi 将获取随机种子的功能和获取随机字节的功能分为了两个不同的方法，因此 NativePRNG 在实现时也分别调用 RandomIO 的不同方法。RandomIO 读取系统熵池也会区分不同文件，根据随机种子文件来源和随机数文件来源的不同组合分为三类，分别对应枚举类 Variant 的三种类型。

  • MIXED，默认情况，对应 NativePRNG 类本身，随机种子文件默认为 /dev/random，随机数文件则固定使用 /dev/urandom。其中，随机种子文件可以更改，决定因素正是 SunEntries.seedSource 属性，因此可以手动配置。随机数文件无法更改。
  • BLOCKING，对应内部类 NativePRNG$Blocking，同时使用 /dev/random 作为随机种子文件和随机数文件。
  • NONBLOCKING，对应内部类 NativePRNG$NonBlocking，同时使用 /dev/urandom 作为随机种子文件和随机数文件。
类型 随机种子文件 随机数文件
MIXED /dev/random（默认配置，可以修改） /dev/urandom
BLOCKING /dev/random /dev/random
NONBLOCKING /dev/urandom /dev/urandom

RandomIO 封装了对熵池文件的读取操作，可以从系统熵池读取对应的真随机字节，但并非完全依赖于系统熵池。RandomIO 内部还持有了一个 SHA1PRNG 伪随机算法的实例（即 sun.security.provider.SecureRandom），对外提供随机字节时会结合系统熵池的真随机数据和 SHA1PRNG 算法生成的伪随机数据，确切地说是对两者采取异或运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private static class RandomIO {
    // get pseudo random bytes
    // read from "next" and XOR with bytes generated by the
    // mixing SHA1PRNG
    private void implNextBytes(byte[] data) {
        // 简化代码
        try {
            // 调用 SHA1PRNG 算法填充 data 数组
            getMixRandom().engineNextBytes(data);
            // 从系统熵池读取真随机随机字节，复制进 localBuffer
            ensureBufferValid();
            localBuffer = Arrays.copyOfRange(...);
            // 混合两个随机数组，异或运算
            int len = 0;
            while (len < data.length) {
                data[ofs] ^= localBuffer[localofs];
            }
        } catch (IOException e){
            throw new ProviderException("nextBytes() failed", e);
        }
    }
}

结合上述两小节的内容，我们可以知道 SecureRandom 的大致逻辑。

SecureRandom 类采取了配置化的设计，可以在两大类随机数生成算法中选择：SHA1PRNG 是偏向计算的伪随机数算法，NativePRNG 则是基于系统熵池的算法，还可以配置为读取不同的系统熵池以避免阻塞。

Unix-Like 平台默认使用 NativePRNG 算法，也就是以 /dev/random 和 /dev/urandom 两个文件作为熵源。即使明确指定使用系统熵池，SecureRandom 也并非直接返回从熵池读取到的随机字节，还会用 SHA1PRNG 算法来掺入随机因子。

SHA1PRNG 的实现

对应实现类为 sun.security.provider.SecureRandom，与 java.security.SecureRandom 同名，后续为了区分，均称呼其为 SHA1PRNG。SHA1PRNG 继承自 SecureRandomSpi，利用哈希算法生成随机序列，换而言之，这是一个伪随机数生成器。上文曾提及，有两种方式生成密码学安全的随机数，其中一种是“真随机种子 + 密码学安全的伪随机算法”，这正是 SHA1PRNG 的主要思想。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/** JDK 8 */
public final class SecureRandom extends SecureRandomSpi
implements java.io.Serializable {
    /** 生成随机种子 */
    @Override
    public byte[] engineGenerateSeed(int numBytes) {
        byte[] b = new byte[numBytes];
        // 调用 SeedGenerator
        SeedGenerator.generateSeed(b);
        return b;
    }

    /** 懒加载 seeder 的技巧 */
    private static class SeederHolder {
        // 访问 seeder 时会触发类初始化
        private static final SecureRandom seeder;

        static {
            seeder = new SecureRandom(SeedGenerator.getSystemEntropy());
            byte [] b = new byte[DIGEST_SIZE];
            // 调用 SeedGenerator
            SeedGenerator.generateSeed(b);
            seeder.engineSetSeed(b);
        }
    }

    @Override
    public synchronized void engineNextBytes(byte[] result) {
        // 如果没有提供种子，第一次调用时 state 就会为 null
        if (state == null) {
            byte[] seed = new byte[DIGEST_SIZE];
            // 注意上面注释，此处会调用 SeedGenerator
            SeederHolder.seeder.engineNextBytes(seed);
            state = digest.digest(seed);
        }

        // 省略后续代码
    }
}

SHA1PRNG 类的代码主要是对于 SHA1 哈希算法的运用，我们重点关注 SeedGenerator。不管是生成种子还是生成随机字节，都会调用种子生成器 SeedGenerator 的静态方法 generateSeed()。

1
2
3
4
5
6
7
8
9
10
11
/** JDK 8 */
package sun.security.provider;
abstract class SeedGenerator {
    private static SeedGenerator instance;

    static public void generateSeed(byte[] result) {
        instance.getSeedBytes(result);
    }

    abstract void getSeedBytes(byte[] result);
}

SeedGenerator 是个抽象类，有两种子类。

  • ThreadedSeedGenerator，启动多个子线程，利用子线程产生的随机噪声生成随机数据。这种实现不依赖外部文件，移植性较高。
  • URLSeedGenerator，从指定文件中读取字节。这种实现涉及到外部文件，需要系统保证功能一致，移植性较差。
    • NativeSeedGenerator，Unix-Like 系统与 URLSeedGenerator 实现一致，从系统熵池文件读取随机字节，Windows 系统则使用 MS CryptoAPI 来生成随机字节。

SeedGenerator 类中，会对静态属性 instance 进行初始化，初始化时也会参考“老朋友” SunEntries.seedSource 的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
static {
    // here!
    String egdSource = SunEntries.getSeedSource();

    if (egdSource.equals(SunEntries.URL_DEV_RANDOM) ||
        egdSource.equals(SunEntries.URL_DEV_URANDOM)) {
        // 如果使用系统熵池，则对应 NativeSeedGenerator
        instance = new NativeSeedGenerator(egdSource);
    } else if (egdSource.length() != 0) {
        // 非系统熵池文件作为随机源
        instance = new URLSeedGenerator(egdSource);
    }

    // Fall back to ThreadedSeedGenerator 兜底
    if (instance == null) {
        instance = new ThreadedSeedGenerator();
    }
}

代码层次比较清晰，先尝试获取系统配置，如果配置中指定了随机种子文件，就会构造 NativeSeedGenerator 对象；如果没有配置或者初始化失败，就会构建一个移植性最好的 ThreadedSeedGenerator 对象。

使用 SHA1PRNG 算法就不会阻塞了吗？显然，如果指定了 seedSource，还是可能读取 /dev/random 或 /dev/urandom，仍然可能阻塞。

至此，我们可以对 Windows 平台的安全随机工具进行总结。由于 Windows 平台没有提供熵池接口，无法使用 NativePRNG 算法，因此默认使用的是 SHA1PRNG 算法，并且 SeedGenerator 使用的是基于系统 API 的 NativeSeedGenerator。

需要使用 SecureRandom.getInstanceStrong() 吗？

SecureRandom 类提供了许多静态工厂方法，用于快速获取指定的随机数生成器。

1
2
3
4
public static SecureRandom getInstance(String algorithm)
public static SecureRandom getInstance(String algorithm, String provider)
public static SecureRandom getInstance(String algorithm, Provider provider)
public static SecureRandom getInstanceStrong()

三种 getInstance() 方法只是普通的工厂方法，用于指定随机数算法，比如指定为 SHA1PRNG、NativePRNG、NativePRNGBlocking、NativePRNGNonBlocking。对于后两种算法而言，由于不是默认算法之一，主动指定是唯一的使用入口。

1
2
3
4
SecureRandom sr1 = SecureRandom.getInstance("NativePRNGBlocking");
System.out.println(sr1.nextInt());
System.out.println(sr1.nextInt());
System.out.println(sr1.nextInt());

比较特殊的是 getInstanceStrong()，从方法名上看，似乎是安全性比较高的随机数生成器。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public static SecureRandom getInstanceStrong() throws NoSuchAlgorithmException {
    String property = Security.getProperty("securerandom.strongAlgorithms");
    String remainder = property;
    while (remainder != null) {
        Matcher m;
        // 正则表达式匹配
        if ((m = StrongPatternHolder.pattern.matcher(remainder)).matches()) {
            String alg = m.group(1);
            String prov = m.group(3);

            try {
                if (prov == null) {
                    return SecureRandom.getInstance(alg);
                } else {
                    return SecureRandom.getInstance(alg, prov);
                }
            } catch (NoSuchAlgorithmException |
                     NoSuchProviderException e) {
            }

            // 出错了换下一组配置继续匹配
            remainder = m.group(5);
        } else {
            remainder = null;
        }
    }

    throw new NoSuchAlgorithmException(
        "No strong SecureRandom impls available: " + property);
}

根据代码，该方法从安全配置中获取 securerandom.strongAlgorithms 属性，然后从该配置值中提取算法和实现，最后用 getInstance() 工厂方法构建实例。而 securerandom.strongAlgorithms 配置在哪呢，就在前面出现过的 JDK 配置文件 java.security 中。

1
2
> cat java.security | grep 'securerandom.strongAlgorithms'
securerandom.strongAlgorithms=NativePRNGBlocking:SUN,DRBG:SUN

默认的算法为 NativePRNGBlocking，我们已经知道该算法以 /dev/random 同时作为随机种子文件和随机数文件。

所以，需要使用 SecureRandom.getInstanceStrong() 吗？getInstanceStrong() 也是使用了系统熵池文件作为随机源，并非真的更安全，与普通构造函数创造的对象没什么明显区别。相反，由于使用了 /dev/random，存在熵池耗尽而阻塞的可能。

SecureRandom 的阻塞问题

由于 SecureRandom 在某些情况下会使用系统熵池 /dev/random，存在因为熵池耗尽而阻塞的可能性。这种阻塞严重时会持续几分钟，这对于系统性能的影响十分明显，我们必须尽量避免这种情况。

以 Linux 系统的 JDK 为例，以下情况 SecureRandom 可能阻塞：

  • getInstance("NativePRNGBlocking") 指定使用 NativePRNGBlocking 算法，此时生成随机数或生成随机种子时都可能阻塞，类似的情况还有 SecureRandom.getInstanceStrong() 方法；
  • 默认情况下，也就是使用 NativePRNG 算法的 MIXED 模式，生成随机种子时可能阻塞（调用 generateSeed(int numBytes) 方法）；
  • 使用 SHA1PRNG 算法时，如果采用系统默认配置，内部的种子生成器的实际类型是使用了 /dev/random 的 NativeSeedGenerator，存在阻塞的可能性。

针对后面两种默认配置的阻塞情况，可以手动更换随机种子源为 /dev/random，比如在 JVM 启动命令中指定 -Djava.security.egd=file:/dev/urandom，或者修改 JDK 配置文件 java.security 为 securerandom.source=file:/dev/urandom。

SecureRandom 发生阻塞时，可以通过 jstack 命令可以获取阻塞线程的栈，大致如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
"main" #1 prio=5 os_prio=0 tid=0x00007f894c009000 nid=0x1129 runnable [0x00007f8952aa9000]
java.lang.Thread.State: RUNNABLE
    at java.io.FileInputStream.readBytes(Native Method)
    at java.io.FileInputStream.read(FileInputStream.java:255)
    at sun.security.provider.NativePRNG$RandomIO.readFully(NativePRNG.java:424)
    at sun.security.provider.NativePRNG$RandomIO.ensureBufferValid(NativePRNG.java:525)
    at sun.security.provider.NativePRNG$RandomIO.implNextBytes(NativePRNG.java:544)
    - locked <0x000000076c77cb28> (a java.lang.Object)
    at sun.security.provider.NativePRNG$RandomIO.access$400(NativePRNG.java:331)
    at sun.security.provider.NativePRNG$Blocking.engineNextBytes(NativePRNG.java:268)
    at java.security.SecureRandom.nextBytes(SecureRandom.java:468)
    at java.security.SecureRandom.next(SecureRandom.java:491)
    at java.util.Random.nextInt(Random.java:390)
    at TestRandom.main(TestRandom.java:12)

如果线程栈中出现了 SecureRandom 相关的 locked 提示，那么阻塞原因很可能就与之相关。从上述栈信息可知，这是指定了 NativePRNGBlocking 算法的 SecureRandom 对象，在生成随机数时阻塞。阻塞时线程状态仍然为 RUNNABLE，因为 JVM 不会修改调用阻塞式 API 时阻塞的线程状态，这种阻塞仅仅能从系统层面观测到。

有常见的一种情况为 Tomcat 启动时阻塞，线程栈大致如下：

1
2
3
4
5
6
7
8
9
10
"main@1" prio=5 tid=0x1 nid=NA runnable
  java.lang.Thread.State: RUNNABLE
      at java.io.FileInputStream.readBytes(FileInputStream.java:-1)
      at java.io.FileInputStream.read(FileInputStream.java:255)
      at sun.security.provider.SeedGenerator$URLSeedGenerator.getSeedBytes(SeedGenerator.java:539)
      at sun.security.provider.SeedGenerator.generateSeed(SeedGenerator.java:144)
      at sun.security.provider.SecureRandom$SeederHolder.<clinit>(SecureRandom.java:203)
      at sun.security.provider.SecureRandom.engineNextBytes(SecureRandom.java:221)
      - locked <0x1af3> (a sun.security.provider.SecureRandom)
      at java.security.SecureRandom.nextBytes(SecureRandom.java:468)

从栈信息可知，这里使用了 SHA1PRNG 算法（sun.security.provider.SecureRandom 可知），但是种子生成器使用的是 URLSeedGenerator（准确点应该是 NativeSeedGenerator），在生成种子时由于熵池耗尽产生了阻塞问题。Tomcat 使用了 SecureRandom 的类为 org.apache.catalina.util.StandardSessionIdGenerator，具体代码在其抽象父类 SessionIdGeneratorBase 中。Tomcat 生成 sessionId 时，处于安全考虑，使用 SHA1PRNG 算法实现的 SecureRandom 类，在获取种子时产生阻塞。从代码的注释可知，Tomcat 选取 SHA1PRNG 作为默认算法的原因也颇为无奈：一来足够快，二来跨平台性最好。

解决阻塞问题的核心就是避免使用 /dev/random，可以通过工厂方法创建使用了非阻塞算法的对象，也可以修改系统配置，使用 /dev/urandom 作为种子源。根据实际情况灵活应变即可。

除此之外，还可以使用 Linux 的 haveged 守护进程进行噪声补充，保证熵池中随时都有足够资源。

最佳实践

Random 最佳实践

了解过实现原理后，我们已知 Random 采取的是线程安全版的 LGC 算法，利用“循环 + CAS”的方式保证线程安全，可以在多个线程中使用一个 Random 对象。在并发性很高的情况下，“循环 + CAS”存在非常高的竞争，导致性能下降。因此现在更推荐使用线程本地存储的 ThreadLocalRandom。

ThreadLocalRandom 同样是一个伪随机数生成器，不支持构建函数创建，只能通过静态方法获取对象 ThreadLocalRandom t = ThreadLocalRandom.current()，使用与 Random 类似，但不支持设置种子。

current() 方法获取到的对象为全局单例对象，也就是所有的线程获取到的实际上是同一个对象，但 ThreadLocalRandom 巧妙地将各线程本地状态存储在线程对象中，读写时再通过 Unsafe 类来操作，从而实现一个单例对象为不同线程提供服务。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class ThreadLocalRandom extends Random {
    // Unsafe 相关
    private static final Unsafe U = Unsafe.getUnsafe();
    private static final long SEED
        = U.objectFieldOffset(Thread.class, "threadLocalRandomSeed");
    private static final long PROBE
        = U.objectFieldOffset(Thread.class, "threadLocalRandomProbe");

    private static final ThreadLocalRandom instance = new ThreadLocalRandom();
    public static ThreadLocalRandom current() {
        if (U.getInt(Thread.currentThread(), PROBE) == 0)
            // 如果当前线程是第一次使用，则会进行一次种子初始化操作
            localInit();
        return instance;
    }

    static final void localInit() {
        int p = probeGenerator.addAndGet(PROBE_INCREMENT);
        int probe = (p == 0) ? 1 : p; // skip 0
        long seed = RandomSupport.mixMurmur64(
                seeder.getAndAdd(SEEDER_INCREMENT));
        Thread t = Thread.currentThread();
        // Unsafe 修改 t 对象的属性
        U.putLong(t, SEED, seed);
        U.putInt(t, PROBE, probe);
    }
}

每次调用 nextXXX 方法时，都会从 Thread 对象中获取对应属性，修改后又会写回 Thread 对象中，让 Thread 对象承担了帮 ThreadLocalRandom 存储状态的功能。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// Thread 类中的相关属性
public class Thread implements Runnable {
    /** The current seed for a ThreadLocalRandom */
    @jdk.internal.vm.annotation.Contended("tlr")
    long threadLocalRandomSeed;

    /** Probe hash value; nonzero if threadLocalRandomSeed initialized */
    @jdk.internal.vm.annotation.Contended("tlr")
    int threadLocalRandomProbe;

    /** Secondary seed isolated from public ThreadLocalRandom sequence */
    @jdk.internal.vm.annotation.Contended("tlr")
    int threadLocalRandomSecondarySeed;
}

以“抢红包”场景为例。设置红包总额和份数后，每次请求都会获取一个随机额度的红包。有很多方法可以实现这个功能，比如“预先分配”，创建红包时生成所有红包额度序列，请求时直接返回一个值即可；也可以“临时分配”，即每次请求时再临时计算单个红包额度。两者区别在于存储方面，预先分配的方式需要存储的数据更多，一个额度序列，以及记录当前未发出红包的指针，而临时分配仅需保存剩余金额和剩余个数，一个红包仅占一条记录，空间占用显然比前者小。

临时分配策略有很多种，一种比较符合情理的策略为：在 0.01 和剩余金额的两倍之间取一个随机值。这样不一定能保证公平，但能保证符合社会学的“公平分配”，毕竟不患寡而患不均，标准差才是重中之重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
public class RedPacketAllocator {

    /**
     * 取 1 到平均值的两倍之间的一个随机值
     */
    public static final RedPacketStrategy WX_STRATEGY = (total, count) -> {
        if (count == 1) {
            return total;
        }
        int max = total / count * 2;
        int money = (int) (ThreadLocalRandom.current().nextDouble() * max);
        return Math.max(1, money);
    };

    private final RedPacketStrategy strategy;
    /** 金额乘 100 保存 */
    private int leftMoneyx100;
    private int leftCount;

    public RedPacketAllocator(int total, int count) {
        this(WX_STRATEGY, total, count);
    }

    public RedPacketAllocator(RedPacketStrategy strategy,
                              int total, int count) {
        this.strategy = strategy;
        this.leftMoneyx100 = total * 100;
        this.leftCount = count;
    }

    public synchronized double nextMoney() {
        if (leftCount <= 0) {
            throw new IllegalStateException("No money left.");
        }

        int money = strategy.nextMoney(leftMoneyx100, leftCount);
        leftMoneyx100 -= money;
        leftCount--;

        return money / 100.0;
    }

    /**
     * 红包分配算法，计算下一个红包额度
     */
    @FunctionalInterface
    public interface RedPacketStrategy {

        /**
         * 根据总额和份数计算下一个红包额度
         *
         * @param total 总额
         * @param count 份数
         * @return int 最小为 1
         */
        int nextMoney(int total, int count);
    }
}

SecureRandom 最佳实践

SecureRandom 主要用在密码领域，最重要的一点就是要避免阻塞，可以根据具体场景采取不同的措施避免阻塞。其次则是可以定期对生成器进行一次种子注入，以提高安全性。

一个简单例子，敏感数据“加盐”场景。对于用户密码等敏感数据，需要进行“加盐”处理后再存储，这样能避免数据泄漏的风险。所谓盐者，就是一个随机数据，将密码与“盐”混合，然后进行一次哈希处理。存储数据时，仅存储“盐”值和哈希处理的结果，用户登录时重新进行一次加盐哈希，如果结果与数据库中记录匹配，则证明密码匹配。
$$
Hash(Hash(password) + salt)
$$
以下代码展示了生成“盐”值的方式，调用方法达到一定次数后会进行一次 Reseed，补充生成器的随机度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
private synchronized byte[] generateSalt() {
    if (null == rng) {
        rng = new SecureRandom();
        log.info("Initialized a random number stream using {} provided by {}",
                rng.getAlgorithm(), rng.getProvider());
        rngUses = 0;
    }
    if (rngUses++ > RESEED_INTERVAL) {
        // 使用一定次数后，重新设置种子，增加安全性
        log.debug("Re-seeding the RNG");
        rng.setSeed(rng.generateSeed(SEED_BYTES));
        rngUses = 0;
    }
    salt = new byte[SALT_BYTES];
    rng.nextBytes(salt);
    return salt;
}

End

从古老的龟甲占卜到现在各种彩票奖券，尽管世界越来越追求有序，人类仍在向混沌寻求某种希望，这也正是随机事件所具备的宿命感的魅力。

回到最初的问题，计算机掷骰子吗？相信此刻每一位读者已经有了答案。计算机和人脑一样，并不会凭空生成随机数，但可以借助数学工具，生成看似随机实则具备周期规律的伪随机数；还可以依赖客观世界中的不确定性，生成真随机数。

参考

[1] Linear congruential generator - Wikipedia

[2] The Right Way to Use SecureRandom · Terse Systems

[3] The Java SecureRandom Class | Baeldung

[4] 再谈随机数引起的阻塞问题 | 夜行船

[5] 一个JAVA应用启动缓慢问题排查 –来自jdk securerandom 的问候 - 腾讯云开发者社区-腾讯云

[6] 解决SecureRandom.getInstanceStrong()引发的线程阻塞问题_java_脚本之家